7714. Milling machines

 

A Fab Lab is a small open workshop where you can create or manufacture almost anything you want, mainly using computer-controlled tools such as a laser cutter or a 3D printer. Recently, the FAU Fab Lab acquired a CNC milling machine. With this machine, you can cut or remove material from the surface of a workpiece using various tools. The entire process is controlled by a computer program.

Sometimes I wondered what would happen if several workpieces of different shapes were processed using the same milling program. To simplify the situation, let’s assume that we only have two-dimensional workpieces without holes. A milling program consists of several steps, each describing which parts of the surface the milling machine should remove material from (using different tools).

 

Input. The first line contains  two integers w and s (1 ≤ w, s ≤ 104) – the number of workpieces and the number of steps in the milling program.

The next line contains two integers x and y (1 ≤ x, y ≤ 100), where x is the width of a workpiece, and y is its maximum possible height.

Each of the following w lines describes one workpiece. The description of each workpiece consists of x non-negative integers defining the surface height in each column.

Then follow s lines describing the milling steps. Each milling step consists of x non-negative integers si (0 ≤ si ≤ y), determining how much material should be removed in each column (relative to the milling area height, i.e., relative to y, not to the top of the workpiece). See the illustration.

 

Output. For each workpiece, print one line containing  integers – the remaining surface heights after all milling steps (in the same order as in the input).

 

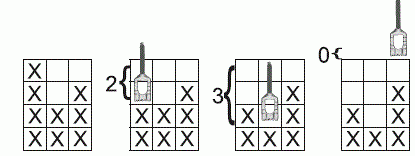
Figure. In the first example, you can see how the second workpiece looks after applying all milling steps sequentially: each value in the program defines the vertical position of the milling head.

 

Sample input 1

Sample output 1

2 1

3 4

4 4 4

4 2 3

2 3 0

2 1 4

2 1 3

 

 

Sample input 2

Sample output 2

1 3

10 100

11 22 33 44 55 66 77 88 99 100

1 100 1 100 1 100 1 100 1 100

58 58 58 58 58 58 58 58 58 58

42 42 42 42 42 42 42 42 66 42

11 0 33 0 42 0 42 0 34 0

 

 

SOLUTION

mathematics

 

Algorithm analysis

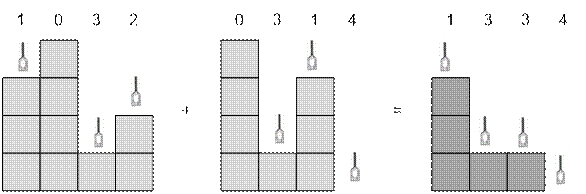
The milling program consists of s steps. Let at the -th step () a layer of thickness mij be removed from the surface in column j (1 ≤ j ≤ x). It is clear that the total amount removed in column j will be

max(m1j, m2j, …, msj)

We’ll call the milling scheme the set of integers

(cuts1, cuts2, …, cutsx),

where

cutsj = max(m1j, m2j, …, msj), 1 ≤ j ≤ x

 

The same milling scheme is applied to all w workpieces. After computing the values of cutsj (1 ≤ j ≤ x), this scheme is then applied sequentially to each workpiece.

 

Algorithm implementation

Declare the arrays. The information about the workpieces is stored in the array detail, and the milling scheme is stored in the array cuts.

 

int detail[10001][101], cuts[101];

 

Read the input data.

 

scanf("%d %d %d %d", &w, &s, &x, &y);

 

Read the information about the w workpieces.

 

for (i = 0; i < w; i++)

for (j = 0; j < x; j++)

  scanf("%d", &detail[i][j]);

 

Read and process the s steps of the milling program. For each position j, the value cuts[j] represents the maximum cutting depth achieved at any of the steps.

 

for (i = 0; i < s; i++)

for (j = 0; j < x; j++)

{

  scanf("%d", &val);

  if (val > cuts[j]) cuts[j] = val;

}

 

The maximum possible height of a workpiece is y. The milling head at position j is lowered to a depth of cuts[j]. Consequently, after milling, the remaining height of the i-th workpiece at position j will be equal to

min(detail[i][j], y – cuts[j]).

 

for (i = 0; i < w; i++)

{

  for (j = 0; j < x; j++)

    printf("%d ", min(detail[i][j], y - cuts[j]));

  printf("\n");

}